1. 생애
- 1238년경 출생하여 1289년경 사망함. (중국의 남송 시대)
- 남송의 향주 근처 전당에서 태어나 남송에서 주로 활동.
- 별로 알려진 바가 없으나, 뛰어난 수학교사였거나 청렴한 하급 관리였을 것으로 추측.
2. 업적
- 마방진 연구 : 동양문화권에서 마방진은 역(易)과 역(曆)이 관련되어 신비주의사상이 되었다. 이것을 연신방위도(年神方位圖)라고 한다. 특히 조선시대의 기본 산서로 사용되던 ‘양휘산법(楊輝算法)’에는 여러 개의 방진이 소개되어 있다.
- 양휘의 삼각형 발견 : ‘양휘의 삼각형’은 ‘파스칼의 삼각형’과 같은 것으로서, 양휘는 파스칼보다 400년 정도 앞서 이를 발견하였다.
3. 논문 및 저서
- 상해구장산법(詳解九章算法) : 유휘와 이순풍이 주해한 ‘구장산술’의 246개 문제 중 80개를 선정하여 문제를 새로운 방법으로 분류하거나 기하학적 접근을 통해 몇 가지 급수에 대한 공식을 이끌어내는 시도를 하였다.
- 양휘산법(楊輝算法) : 양휘가 쓴 ‘승제통변산보(乘除通變算寶)’ 3권(1274), ‘속고적기산법(續古適奇算法)’ 2권(1275) 및 ‘전무비류승제첩법(田畝比類乘除捷法)’ 2권(1275)의 책을 하나로 엮은 수학서이다. 이론 중심의 전문서적이 아닌 일종의 계몽서로 실생활에 필요한 중요한 계산 방법과 문제를 수록하였다. 조선시대 중인들이 기술직 고시에 해당하는 잡과의 시험 과목 중 하나이기도 하였다.
4. 학교수학과 관련하여 참고할 점
‘양휘산법’의 내용 중 중학교 수학과 관련된 문제는 다음과 같다.
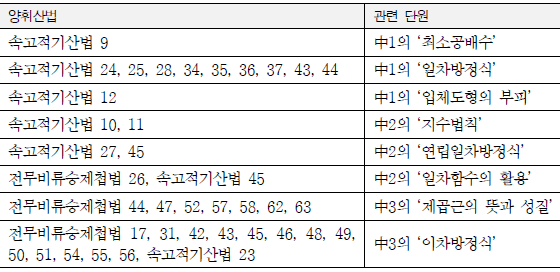
예제. 큰딸은 사흘에 한 번씩 집에 들르고, 가운데 딸은 나흘에 한 번씩 집에 들르고, 막내딸은 닷새에 한 번씩 집에 들른다고 하면 며칠마다 모두 만나겠는가? (속고적기산법 9)
예제. 쌀 창고의 동서가 24자, 남북이 36자, 높이가 18자라면, 곡식을 얼마나 저장할 수 있겠는가? (속고적기산법 12)
참고 : 이광연․방지혜․이유호, 양휘산법과 중학교 수학의 방정식과 함수 영역의 비교, East Asian Mathematical Journal Vol. 27 (2011), No.2, pp.243-259