예각삼각형의 외심으로부터 세 변까지의 거리의 합은 외접원의 반지름과 내접원의 반지름의 합과 같다.
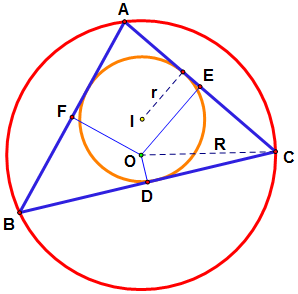
즉 위 그림과 같이 예각삼각형 ABC에서 내심을 I, 외심을 O라고 하고 외심에서 세 변에 내린 수선의 발을 D, E, F라고 하자. 또한 내접원의 반지름을 r, 외접원의 반지름을 R라고 하자. 그러면
가 성립한다.
증명. 꼭짓점 A. B. C가 마주보는 변의 길이를 각각 a, b, c라고 하자. 외심과 내심의 성질에 의하여
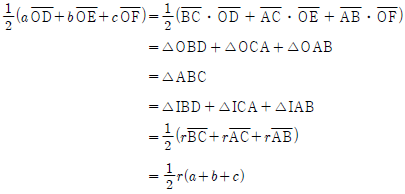
이므로
가 성립한다.
이제 꼭짓점 A, B, C에서 각 대변에 내린 수선의 발을 각각 X, Y, Z라고 하자.
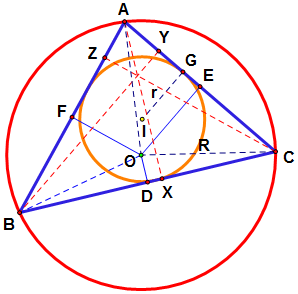
외심의 성질에 의하여 2∠ABX = ∠AOC = 2∠AOE 이므로
이고, 따라서
이다. 그러므로
이다. 비슷한 방법으로
를 얻는다. (2), (3), (4)를 변마다 더하면
를 얻는다. (1)과 (5)를 변마다 더하면
를 얻는다. 이 등식의 양변을 (a+b+c)로 나누면
를 얻는다. (증명 끝)